Euler walk in a n-ary tree
21 Dec 2021
Euler walk in a tree involves visiting all nodes of the tree exactly once and child nodes in a Depth First pattern. The nodes are recorded in a list when we visit the node as well as when we move away from it.
This type of list (Euler Path) is useful when you want to unwrap the tree structure in a linear way to perform range queries in competitive programming problems.
In the sample implementation below, I have shown DFS using recursion as well as an iterative approach to visit every node and create an Euler path array.
Recursion approach- Prefer for simplicity and ease of understanding.Iterative approach- Prefer for walking trees that have a large number of levels/depth (i.e., the root is at level 0 and its direct children at level 1 etc.,) where recursive DFS will end up in stack overflow error.
Let us consider an n-ary tree with 7 nodes as shown below, the Euler walk directions are shown using highlighted arrows
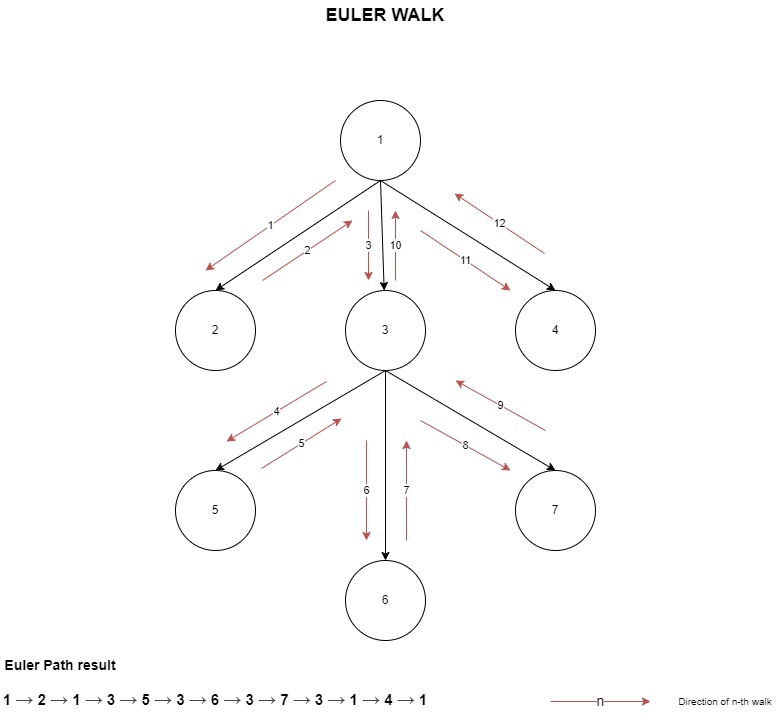
Code Snippet
EulerWalk.cs
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace Algorithms.Tree
{
/// <summary>
/// Euler walk in an undirected tree
/// Ref: https://davidsekar.com/algorithms/euler-walk-in-a-n-ary-tree
/// </summary>
public class EulerWalk
{
// Euler Walk ( preorder traversal) converting tree to linear depthArray Time Complexity : O(n)
public List<int> Dfs(List<List<int>> adjacent, int current, int previous, List<int> euler)
{
// Pushing root to euler walk
euler.Add(current);
foreach (var x in adjacent[current])
{
// Just avoid moving back to previous node, without checking for children
if (x != previous)
{
Dfs(adjacent, x, current, euler);
// Pushing current again in backtrack of euler walk
euler.Add(current);
}
}
return euler;
}
public List<int> DfsNonRecursive(List<List<int>> adjacent)
{
var maxSize = adjacent.Count;
var euler = new List<int>(2 * maxSize); // Max capacity = 2*N-1
var visited = new bool[maxSize];
var nodesToVisit = new Stack<int>();
var childCount = new int[maxSize + 1];
nodesToVisit.Push(1); // Add root index where the walk begins
while (nodesToVisit.Count > 0)
{
var node = nodesToVisit.Peek();
euler.Add(node);
visited[node] = true;
while (true)
{
if (adjacent[node].Count == childCount[node])
{
// Nodes are removed from stack, when there are no more children to visit
nodesToVisit.Pop();
break;
}
// Avoid pushing already visited nodes
var next = adjacent[node][childCount[node]];
childCount[node]++;
if (!visited[next])
{
nodesToVisit.Push(next);
break;
}
}
}
return euler;
}
}
}
EulerWalkTests.cs - It is just to show the simple usage
using Algorithms.Tree;
using Microsoft.VisualStudio.TestTools.UnitTesting;
using System.Collections.Generic;
namespace AlgorithmTests.Tree
{
[TestClass]
public class EulerWalkTests
{
[TestMethod]
[DynamicData(nameof(EulerPathTestData), DynamicDataSourceType.Method)]
public void DfsNonRecursiveTests(List<List<int>> adjacentNodes, List<int> expected)
{
var eulerPath = new EulerWalk().DfsNonRecursive(adjacentNodes);
CollectionAssert.AreEqual(expected, eulerPath);
}
[TestMethod]
[DynamicData(nameof(EulerPathTestData), DynamicDataSourceType.Method)]
public void DfsRecursiveTests(List<List<int>> adjacentNodes, List<int> expected)
{
var eulerPath = new EulerWalk().Dfs(adjacentNodes, 1, -1, new List<int>());
CollectionAssert.AreEqual(expected, eulerPath);
}
public static IEnumerable<object[]> EulerPathTestData()
{
// There are 7 nodes in the n-ary tree and children of each node given below This is a
// n-ary tree indexed from 1
yield return new object[] {
new List<List<int>>()
{
new List<int>(), // Just a dummy entry for 0 index, as the tree starts from 1
new List<int>() { 2, 3, 4 }, // Children of Root node (1)
new List<int>() { }, // Children of node (2)
new List<int>() { 5, 6, 7 }, // Children of node (3)
new List<int>() { }, // Children of node (4)
new List<int>() { }, // Children of node (5)
new List<int>() { }, // Children of node (6)
new List<int>() { } // Children of Root node (7)
},
new List<int> { 1, 2, 1, 3, 5, 3, 6, 3, 7, 3, 1, 4, 1 }
};
}
}
}
